1.4.9
在 $\mathbb{R}^2$ 中, 对 $\forall x = (x_1, x_2) \in \mathbb{R}^2$, 定义范数
$$
\|x\| = \max(|x_1|, |x_2|),
$$
并设 $e_1 = (1, 0)$, $x_0 = (0, 1)$. 求 $a \in \mathbb{R}$ 适合
$$
\|x_0 - a e_1\| = \min_{\lambda \in \mathbb{R}} \|x_0 - \lambda e_1\|,
$$
并问这样的 $a$ 是否唯一? 请对结果做出几何解释.
📝证明
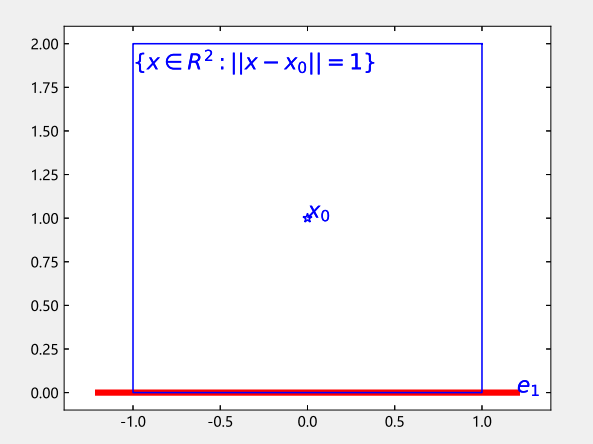
不唯一,
$x_0-\lambda e_1$ 对应
$xOy$ 坐标系中
$y=1$ 的直线, 而在该范数定义下, $\Vert (a,1) \Vert=
$$
\begin{cases}
1,\quad a\in[-1,1] \\
|a|,\quad |a|>1
\end{cases}
$$
$ 于是当 $a\in[-1,1]$ 时均满足条件, 不唯一.
1.4.10
求证: 范数的严格凸性等价于下列条件:
$$
\|x + y\| = \|x\| + \|y\| \quad (\forall x \ne 0, y \ne 0) \implies x = c y \quad (c > 0).
$$
📝证明
"
$\Rightarrow$": 考虑
$\Vert x+y \Vert=\norm{\dfrac{x}{\Vert x \Vert}\Vert x \Vert+\dfrac{y}{\Vert y \Vert}\Vert y \Vert}=(\Vert x \Vert+\Vert y \Vert)\norm{\dfrac{x}{\Vert x \Vert}\dfrac{\Vert x \Vert}{\Vert x \Vert+\Vert y \Vert}+\dfrac{y}{\Vert y \Vert}\dfrac{\Vert y \Vert}{\Vert x \Vert+\Vert y \Vert}}$ 如果
$\dfrac{x}{\Vert x \Vert}\neq \dfrac{y}{\Vert y \Vert}$ 那么结合严格凸性可得
$\Vert x+y \Vert<\Vert x \Vert+\Vert y \Vert=\Vert x+y \Vert$ 矛盾, 所以
$\dfrac{x}{\Vert x \Vert}=\dfrac{y}{\Vert y \Vert}$ 即
$x=cy, (c>0)$.
"$\Leftarrow$": 首先范数一定是凸的, 故只需证明严格性. 反设存在 $x,y,\alpha,\beta$ 满足 $\Vert x \Vert=\Vert y \Vert=\alpha+\beta=1, x\neq y$. 有 $\Vert \alpha x+\beta y \Vert=1$. 那么有 $\Vert \alpha x+\beta y \Vert=1=\alpha\Vert x \Vert+\beta\Vert y \Vert\overset{\text{齐次性}}{=}\Vert \alpha x \Vert+\Vert \beta y \Vert$, 于是就有 $\alpha x=c\beta y$, 两边取范数立刻得到 $\alpha=c\beta$, 从而 $x=y$ 矛盾. 故该范数是严格凸的.
1.4.13
设 $\mathscr{X}$ 是 $B^*$ 空间, $\mathscr{X}_0$ 是 $\mathscr{X}$ 的线性子空间, 假定 $\exists c \in (0,1)$, 使得
$$
\inf_{x \in \mathscr{X}_0} \|y - x\| \le c \|y\| \quad (\forall y \in \mathscr{X}).
$$
求证: $\mathscr{X}_0$ 在 $\mathscr{X}$ 中稠密.
📝证明
反设 $\mathscr X_0$ 不稠密, 那么 $\overline{\mathscr X_0}$ 是 $\mathscr X$ 中的真闭子空间, 那么根据 Riesz 引理, 取 $\varepsilon=\frac{1-c}{2}$, 那么存在 $y\in\mathscr X$, 使得 $\Vert y \Vert=1$ 且 $\Vert y-x \Vert\geqslant 1-\varepsilon> c=c\Vert y \Vert\forall x\in \mathscr X_0$ 这就与条件 $\inf \Vert y-x \Vert\leqslant c\Vert y \Vert$ 矛盾. 从而 $\mathscr X_0$ 在 $\mathscr X$ 中稠密.
1.4.14
设 $C_0$ 表示以 0 为极限的实数全体, 并在 $C_0$ 中赋以范数
$$
\|x\| = \max_{n \ge 1} |\xi_n| \quad (\forall x = (\xi_1, \xi_2, \cdots, \xi_n) \in C_0).
$$
又设
$$
M \triangleq \left\lbrace x = \lbrace \xi_n\rbrace _{n=1}^{\infty} \in C_0 \,\middle|\, \sum_{n=1}^{\infty} \frac{\xi_n}{2^n} = 0 \right\rbrace .
$$
- ((1)) 求证: $M$ 是 $C_0$ 的闭线性子空间.
- ((2)) 设 $x_0 = (2, 0, \cdots, 0, \cdots)$, 求证:
$$
\inf_{z \in M} \|x_0 - z\| = 1,
$$
但 $\forall y \in M$ 有 $\|x_0 - y\| > 1$.
📝证明
(1) 取映射
$f:C_0\to \mathbb{R}, f(x)=\sum\limits_{n=1}^\infty \frac{\xi_n}{2^n}$
线性性: 考虑 $\alpha x+\beta y$: $f(\alpha x+\beta y)=\sum\limits_{n=1}^\infty\frac{\alpha\xi_n+\beta\eta_n}{2^n}=\alpha f(x)+\beta f(y)=0$.
于是 $\alpha x+\beta y\in M$.
闭性:由于 $|f(x)|\leqslant\sum\limits_{n=1}^\infty \frac{|\xi_n|}{2^n}\leqslant\Vert x \Vert\sum\limits_{n=1}^\infty \frac{1}{2^n}=\Vert x \Vert$.
所以 $f$ 是连续映射, 又 $\lbrace 0\rbrace $ 是 $\mathbb{R}$ 中的闭集, 所以 $M=f^{-1}(\lbrace 0\rbrace )$ 是闭集.
故 $M$ 是 $C_0$ 的闭线性子空间.
(2) 考虑第一项有 $\Vert x_0-z \Vert\geqslant\max\lbrace |2-\xi_1|,|\xi|\rbrace \geqslant 1$. 所以 $\inf\limits_{z\in M}\Vert x_0-z \Vert=1$.
考虑数列 $x^N=(1-\frac{1}{2^{N-1}},\underbrace{-1,\ldots,-1}_{N\ \text{个}},0,\ldots,0,\ldots)\in M$, 有 $\Vert x_0-x^N \Vert=1+\frac{1}{2^{N-1}}$, 所以下确界取到 1. $\inf\limits_{z\in M}\Vert x_0-z \Vert=1$.
下证 $\forall y\in M$ 有 $\Vert x_0-y \Vert>1$.
考虑反证法, 假设存在序列 $y=(\xi_1,\xi_2,\ldots,\xi_k,\ldots)\in M$, 使得 $\Vert x_0-y \Vert=1$, 则有
$$
\begin{cases}
|\xi_k|\leqslant 1,& k\geqslant 2,\\
2-\xi_1\leqslant 1. &
\end{cases}
$$
$$
所以有
$$
|\sum\limits_{k=2}^\infty \frac{\xi_k}{2^k}|\leqslant\sum\limits_{k=2}^\infty\frac{|\xi_k|}{2^k}\overset{\text{由极限为 0 不可能一直是 1}}{<}\sum\limits_{k=2}^\infty \frac{1}{2^k}=\frac 1 2.
$$
$$
\Rightarrow\left|\frac{\xi_1}{2}\right|=\left|\sum\limits_{k=2}^\infty \frac{\xi_k}{2^k}\right|<\frac{1}{2}\Rightarrow |\xi_1|<1.
$$
这与 $|2-\xi_1|\leqslant 1$ 矛盾.
所以有 $\forall y\in M$ 有 $\Vert x_0-y \Vert>1$.
ℹ️注 1
本题提供一个例子说明: 对于无穷维闭线性子空间来说, 给定其外一点
$x_0$, 未必能在其上找到一点
$y$ 适合
$$
|x_0 - y| = \inf_{z \in M} |x_0 - z|.
$$
换句话说, 给定 $x_0 \notin M$, 未必能在 $M$ 上找到最佳逼近元.
1.4.17
设有商空间 $\mathscr{X} / \mathscr{X}_0$.
- ((1)) 设 $[x] \in \mathscr{X} / \mathscr{X}_0$, 求证: 对 $\forall x \in [x]$, 有
$$
\inf_{z \in \mathscr{X}_0} |x - z| = |[x]|_0.
$$
1. ((2)) 定义映射 $\varphi : \mathscr{X} \to \mathscr{X} / \mathscr{X}_0$ 为
$$
\varphi(x) = [x] \triangleq x + \mathscr{X}_0 \quad (\forall x \in \mathscr{X}),
$$
求证: $\varphi$ 是连续线性映射.
1. ((3)) $\forall [x] \in \mathscr{X} / \mathscr{X}_0$, 求证: $\exists x \in \mathscr{X}$, 使得
$$
\varphi(x) = [x], \quad \text{且} \quad |x| \le 2 |[x]|_0.
$$
1. ((4)) 设 $\mathscr{X} = C[0,1]$, $\mathscr{X}_0 = \lbrace f \in \mathscr{X} \mid f(0) = 0 \rbrace $, 求证:
$$
\mathscr{X} / \mathscr{X}_0 \cong \mathbb{K},
$$
其中记号 “$\cong$” 表示等距同构.
📝证明
- ((1)) $\Vert [x] \Vert=\inf\limits_{y\in [x]}\Vert y \Vert=\inf\limits_{y\in\mathscr X_0}\Vert x+y \Vert=\inf\limits_{z\in\mathscr X_0}\Vert x-z \Vert$.
- ((2)) 根据商空间运算定义, 线性性显然. $\Vert \varphi(x) \Vert_0=\inf\limits_{z\in\mathscr X_0}\Vert x-z \Vert\leqslant\Vert x-0 \Vert=\Vert x \Vert$ 所以 $\varphi(x)$ 连续.
- ((3)) 取代表元 $x'$, 根据 $\Vert [x] \Vert_0=\inf\limits_{z\in\mathscr X_0}\Vert x'-z \Vert$ 所以对任意 $\varepsilon>0$, 存在 $z\in \mathscr X_0$ 使得 $\Vert x'-z \Vert<\Vert [x] \Vert_0+\varepsilon$, 现取 $\varepsilon=\Vert [x] \Vert_0$, 则 $x'+z_0$ 满足 $\varphi(x')=[x],\ \Vert x \Vert\leqslant 2\Vert [x] \Vert_0$.
- ((4)) 取 $T:\mathscr X/\mathscr X_0\to\mathbb K, T([f])=f(0)$. 首先先探究等价类的性质, 若 $f-g\in\mathscr X_0$, 那么有 $f(0)=g(0)$, 所以我们不妨设等价类为 $[f_x]$ 表示所有 $f(0)=x$ 的函数.
先证 $T$ 是线性映射, 即 $T(\alpha [f_x]+\beta [f_y])=T([f_{\alpha x}+f_{\beta y}])=\alpha x+\beta y=\alpha T([f_x])+\beta T([f_y])$. 这一步用到了 $\mathbb{K}$ 的线性性.
再证 $T$ 保范数, 即要证 $\Vert T([f_x]) \Vert=\Vert x \Vert$.
根据定义取 $[f_x]$ 的代表元为 $f,\ f(0)=x$, 有 $\Vert T([f_x]) \Vert=\inf\limits_{g\in\mathscr X_0}\Vert f-g \Vert=\inf\limits_{g\in\mathscr X_0}\max\limits_{t\in[0,1]}|f(t)-g(t)|$
一方面,
$$
\inf\limits_{g\in\mathscr X_0}\max\limits_{t\in[0,1]}|f(t)-g(t)|\geqslant\inf\limits_{g\in\mathscr X_0}|f(0)-g(0)|=|x|
$$
另一方面, 取 $g'=f-x\in \mathscr X_0$, 从而
$$
\inf\limits_{g\in\mathscr X_0}\Vert f-g \Vert\leqslant \Vert f-g' \Vert\overset{\text{恒为 x 的常函数}}{=}\Vert x \Vert,
$$
所以有 $\Vert T([f_x]) \Vert=\Vert x \Vert$.
ℹ️注 2
注意区分上述过程中的范数具体含义.
