1.4.1
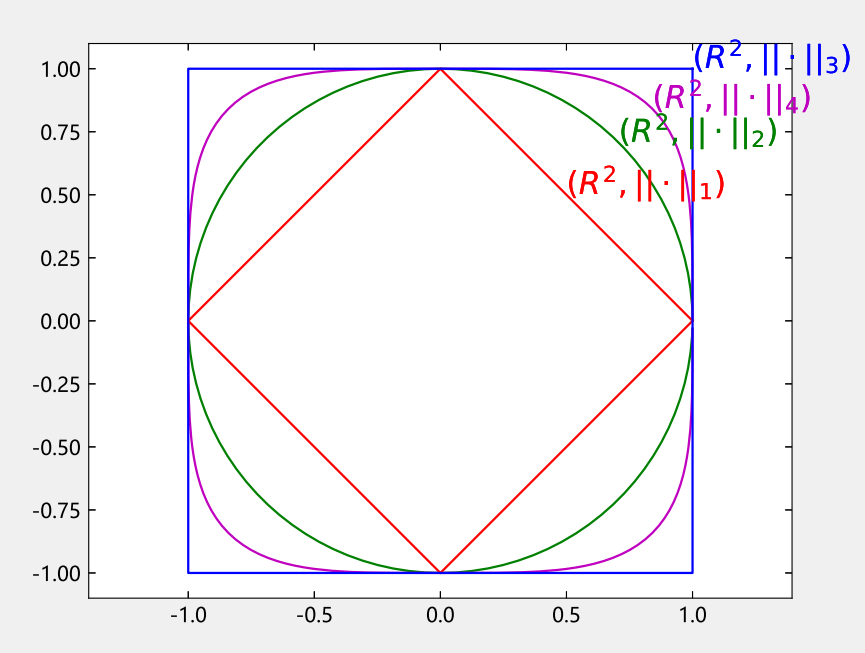
在二维空间 $\mathbb{R}^2$ 中, 对每一点 $z = (x, y)$, 令
(1) 求证 $\|\cdot\|_i$ ($i=1,2,3,4$) 都是 $\mathbb{R}^2$ 的范数.
(2) 画出 $(\mathbb{R}^2, \|\cdot\|_i)$ ($i=1,2,3,4$) 各空间中的单位球面图形.
(3) 在 $\mathbb{R}^2$ 中取定三点 $O = (0,0)$, $A = (1,0)$, $B = (0,1)$, 试在上述四种不同范数下求出 $\triangle OAB$ 三边的长度.
齐次性: $\Vert \alpha z \Vert_1=|\alpha x|+|\alpha y|=\alpha\Vert z_1 \Vert$, $\Vert \alpha z \Vert_2=\sqrt{(\alpha x)^2+(\alpha y)^2}=\alpha\sqrt{x^2+y^2}=\alpha\Vert z \Vert_2$, $\Vert \alpha z \Vert_3=\max(|\alpha x|,|\alpha y|)=\alpha\max(|x|,|y|)=\alpha\Vert z \Vert_3$, $\Vert \alpha z \Vert_4=((\alpha x)^4+(\alpha y)^4)^{1/4}=\alpha (x^4+y^4)^{1/4}=\alpha\Vert z \Vert_4$. 三角不等式: $\Vert z_1+z_2 \Vert_1=|x_1+x_2|+|y_1+y_2|\leqslant |x_1|+|x_2|+|y_1|+|y_2|=\Vert z_1 \Vert_1+\Vert z_2 \Vert_1$, $\Vert z_1+z_2 \Vert_2=\sqrt{(x_1+x_2)^2+(y_1+y_2)^2}\leqslant \sqrt{x_1^2+y_1^2}+\sqrt{x_2^2+y_2^2}=\Vert z_1 \Vert_2+\Vert z_2 \Vert_2$, $\Vert z_1+z_2 \Vert_3=\max(|x_1+x_2|,|y_1+y_2|)\leqslant \max(|x_1|+|x_2|,|y_1|+|y_2|)\leqslant\max(|x_1|,|y_1|)+\max(|x_2|,|y_2|)=\Vert z_1 \Vert_3+\Vert z_2 \Vert_3$, $\Vert z_1+z_2 \Vert_4=((x_1+x_2)^4+(y_1+y_2)^4)^{1/4}\leqslant (x_1^4+y_1^4)^{1/4}+(x_2^4+y_2^4)^{1/4}=\Vert z_1 \Vert_4+\Vert z_2 \Vert_4$. (2)
(3) $\Vert \cdot \Vert_1: 4$, $\Vert \cdot \Vert_2: 2+\sqrt{2}$, $\Vert \cdot \Vert_3: 3$, $\Vert \cdot \Vert_4: 2+\sqrt[4]{2}$.
答案
1.4.2
设 $C(0,1]$ 表示 $(0,1]$ 上连续且有界的函数 $x(t)$ 全体. 对 $\forall x \in C(0,1]$, 令 $\|x\Vert = \sup_{0 < t \leqslant 1} |x(t)|$. 求证:
(1) $\|\cdot\|$ 是 $C(0,1]$ 上的范数;
(2) $l^\infty$ 与 $C(0,1]$ 的一个子空间是等距同构的.
齐次性 $\Vert \alpha x(t) \Vert=\sup\limits_{0<t\leqslant 1}|\alpha x(t)|=\alpha\sup\limits_{0<t\leqslant 1}|x(t)|=\alpha\Vert x(t) \Vert$. 三角不等式: $\Vert x_1(t)+x_2(t) \Vert=\sup\limits_{0<t\leqslant 1}|x_1(t)+x_2(t)|\leqslant \sup\limits_{0<t\leqslant 1}|x_1(t)|+|x_2(t)|\leqslant \sup\limits_{0<t\leqslant 1}|x_1(t)|+\sup\limits_{0<t\leqslant 1}|x_2(t)|=\Vert x_1(t) \Vert+\Vert x_2(t) \Vert$. (2) 构造映射 $T: l^\infty\to C(0,1]$, $\forall \lbrace a_n\rbrace \in l^\infty, T(\lbrace a_n\rbrace )$ 表示 $x(\frac1n)=a_n$ 且用折线段连接 $x(\frac 1n),x(\frac1{n+1})$ 两点的连续函数. 显然这是个单射且像集是 $C(0,1]$ 的子集. 并且由折线段的线性性该映射是线性映射. 下面证其还保范数. 首先对于折线段, 其最大值必取在端点处, 故 $\Vert T(\lbrace a_n\rbrace ) \Vert=\sup x(\frac 1 n)=\sup a_n=\Vert \lbrace a_n\rbrace \Vert$. 所以 $l^\infty$ 与 $C(0,1]$ 的一个子空间 $T(l^\infty)$ 等距同构.证明
1.4.3
在 $C^1[a,b]$ 中, 令
(1) 求证 $\|\cdot\|_1$ 是 $C^1[a,b]$ 上的范数.
(2) 问 $(C^1[a,b], \|\cdot\|_1)$ 是否完备?
三角不等式, 用柯西施瓦茨不等式可得 从而满足. (2) 任取 $c\in (a,b)$, 对于函数 $f(x)=|x-c|\notin C^1[a,b]$, 但函数列 $f_n(x)=\sqrt{(x-c)^2+\frac 1n}$. 有 $|f_n(x)-f(x)|\leqslant\sqrt{\frac1n}$, 从而 $\int_a^b |f_n(x)-f(x)|^2\text{d} x\leqslant (b-a)\frac1n$. 考虑 有 $|f_n'(x)-sgn_c(x)|=|(x-c)|(\frac{1}{|x-c|}-\frac{1}{\sqrt{(x-c)^2+\frac 1 n}})$. 从而 $\Vert f_n-f \Vert=O(\frac{1}{\sqrt n})\to 0$. 即 $\lbrace f_n\rbrace $ 收敛至 $f$, 但 $f\notin C^1[a,b]$ 故不完备.
证明
1.4.4
在 $C[0,1]$ 中, 对每一个 $f \in C[0,1]$, 令
求证: $\Vert \cdot \Vert_1$ 和 $\Vert \cdot \Vert_2$ 是 $C[0,1]$ 中的两个等价范数.
证明
1.4.5
设 $BC[0,\infty)$ 表示 $[0,\infty)$ 上连续且有界的函数 $f(x)$ 全体, 对于每个 $f \in BC[0,\infty)$ 及 $a > 0$, 定义
(1) 求证 $\|\cdot\|_a$ 是 $BC[0,\infty)$ 上的范数.
(2) 若 $a, b > 0$, $a \neq b$, 求证 $\|\cdot\|_a$ 与 $\|\cdot\|_b$ 作为 $BC[0,\infty)$ 上的范数是不等价的.
齐次性: $\Vert \alpha f \Vert=\left(\displaystyle\int_{0}^{\infty} e^{-ax}|\alpha f(x)|^2\text{d} x\right)^{\frac12}=\left(\alpha^2\displaystyle\int_{0}^{\infty} e^{-ax}|f(x)|^2\text{d} x\right)^{\frac12}=\alpha\Vert f \Vert_a$. 三角不等式: 由柯西-施瓦茨不等式, 所以有 $\Vert f+g \Vert_a\leqslant \Vert f \Vert_a+\Vert g \Vert_a$. (2) 不妨设 $a>b>0$ 考虑函数列 从 $n>\frac1b$ 开始定义. 在 $\Vert \cdot \Vert_a$ 中, $\Vert f_n \Vert_a\leqslant \displaystyle\int_{n-\frac 1b}^{n+1+\frac1b}e^{(b-a)x}\text{d} x\leqslant \frac{1}{a-b}e^{(b-a)(n-\frac1b)}$ 由于 $b<a$ 所以 $n\to\infty$ 时 $\frac{1}{a-b}e^{(b-a)(n-\frac{1}{b})}\to 0$, 即 $\Vert f_n \Vert_a\to 0$. 但在 $\Vert \cdot \Vert_b$ 中, $\Vert f_n \Vert_b\geqslant \displaystyle\int_{n}^{n+1}e^{bx-bx}\text{d} x=1$, 从而不收敛, 故两个范数不等价.
证明
1.4.8
记 $[a,b]$ 上次数不超过 $n$ 的多项式全体为 $\mathbb{P}_n$. 求证:
$\forall f(x) \in C[a,b], \exists P_0(x) \in \mathbb{P}_n$, 使得
也就是说, 如果用所有次数不超过 $n$ 的多项式去对 $f(x)$ 一致逼近, 那么 $P_0(x)$ 是最佳的.
证明